This course is meant to give you a comfortable introduction to get warmed up on basic Maths ability, so that you can become confident and comfortable to handle basic Physics. In this course, we aim to give only a fundamental introduction. There is no end to the use of Maths upto the highest level in Physics, all of which cannot be covered here and we suggest further study of advanced Maths if you are interested.
While there are hundreds of courses on the net that explain maths, the important thing is get a feel for ‘y’ as a function of ‘x’ , so that you can use it comfortably anywhere. The first thing is that in maths, ‘y’ is a variable , something that changes, like your height. And another variable is ‘x’, it also can change, let’s say , your age. You know that as you grow from a child to a teenager, you grow taller and taller . In this case, the variable ‘y’ increases with variable ‘x’ ….whether your height increase is a straight line or a curved line, should be a graph of height verus age. This graph of ‘y’ versus ‘x’ is called a FUNCTION. The variable ‘y’ is a function of variable ‘x’ ….
Is it a straight line , i.e. linear ? Or is it a curved line ? We can’t say for sure, it depends on each teenager, how the height varies with his/her age.
A sample graph is shown below for South Asians. It can vary for children in different countries.
Plot ‘y’ on the vertical axis, and ‘x’ on the horizontal axis. You can write the equation as : y=f(x) . That’s all there is to it.

(image courtesy: Research Gate publication , article by Jerome de Wilde et al, 2014)
Now you can see why it is important to know about graphs , and how to handle equations
1) Graphs and equations behind the graph: get comfortable with graphs of various shapes. learn what is slope and how to find it, irrespective of how complex the graph is.
Basic Types of graphs :-
- straight line graph
- exponential curves
- Hyperbolic curves.
Learn what is Maxima and Minima points for curves.
2) Trigonometry :-
- sine, cos and tan.
- example:- sine of a continuously varying angle :- this is applied in physics to a wave equation
3) Integration – what exactly is the physical meaning of Integration. Integration is applied in several chapters of physics theory as well as numericals
4) Differentiation – what exactly is the physical meaning of Differentiation . See in terms of a graph, and how does it help us to handle complex graphs made by equations. Differentiation is applied in several chapters of physics theory as well as numericals
Course Features
- Lectures 30
- Quiz 0
- Duration Lifetime access
- Skill level All levels
- Language English
- Students 182
- Certificate No
- Assessments Yes
- 1 Section
- 30 Lessons
- Lifetime
- Maths starters30
- 1.1Why Maths Starters?
- 1.2Vectors – what are they , How to Add, Subtract, Multiply…..
- 1.3Vectors versus Scalars
- 1.4Vectors – Addition
- 1.5Vectors- Multiplication
- 1.6vectors- Dot Product
- 1.7vectors – Cross-product multiplication and Right Hand Rule
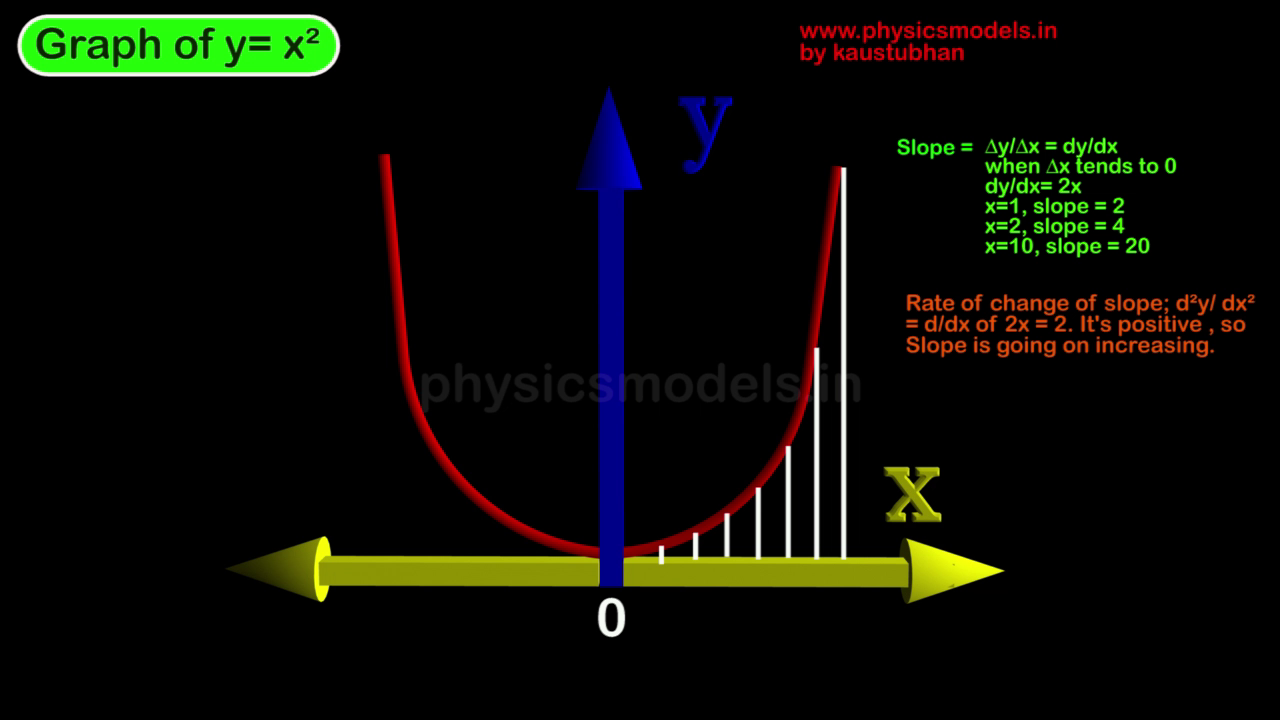
- 1.8graphs and slopes
- 1.9Slope of a graph, why dy/dx
- 1.10Graph – Straight Line type
- 1.11Graph – curved – Exponential type ( Graph – A )
- 1.12Graph-curved-Exponential Type-Graph-B
- 1.13Graph – curved – Exponential Type – Graph – C
- 1.14Graph- Resistivity versus Temperature
- 1.15Graph – Maxima and Minima
- 1.16Graph – Inverted ‘U’ shaped – Thermo-emf versus Temperature
- 1.17Graph- inverted U-shape-Projectile Motion (parabolic)
- 1.18Graph – Hyperbolic type
- 1.19Graph-hyperbolic- Pressure vs Volume (gas compression)
- 1.20Graph – Pressure vs Volume- Carnot Cycle (Thermodynamics)
- 1.21Graph- curves type – for Trigonometric functions
- 1.22Differentiation – why is it useful
- 1.23Differentiation of various functions – summary table
- 1.24Integration- Indefinite integral- example
- 1.25Integration- Definite Integral – example of Gravitational Field calculation
- 1.26Trigonometry basics
- 1.27X-Y-Z axes, planes and vectors
- 1.28Integration formulae summary table
- 1.29Solved problems
- 1.30TRIAL TEST





1 Comment
Nice explanation